Dans quelle situation faut-il standardiser un indicateur?
Quelle est la fréquence de telle ou telle maladie? Quel est le taux d’hospitalisation? À combien s’élèvent les coûts pour le secteur de la santé? Pour bon nombre de chiffres en lien avec la santé, la comparaison n’est pertinente que si l’on connaît la taille de la population à laquelle ils se rapportent. C’est pourquoi nous calculons des parts en pour-cent ou des taux qui fournissent des chiffres pour 1000 ou pour 100 000 habitants (taux bruts).
Les questions portant sur les différences entre les régions ou selon les groupes de population suscitent un vif intérêt. Il en va de même pour l’évolution de ces taux au fil du temps. Pour corriger l’effet des différences dans la composition de la population, il faut tenir compte des caractéristiques structurelles que sont l’âge et le sexe lors des comparaisons. Ainsi, on peut s’attendre à ce qu’une population très âgée soit plus affectée par certaines maladies qu’une population plus jeune, et donc que le taux d’hospitalisation et les coûts de santé soient plus élevés. De même, le nombre d’hospitalisations est plus élevé chez les femmes en âge de procréer que chez les hommes du même groupe d’âge.
Si des différences notables dans la structure démographique des populations s’observent surtout dans un contexte international, force est de constater que dans notre pays, des différences apparaissent d’un canton à l’autre. En 2022, le Tessin comptait davantage de personnes âgées de 65 ans ou plus (24%) que le canton de Fribourg (17%), voir graphique 1. Bien sûr, la structure de la population d’une région peut aussi évoluer avec le temps.
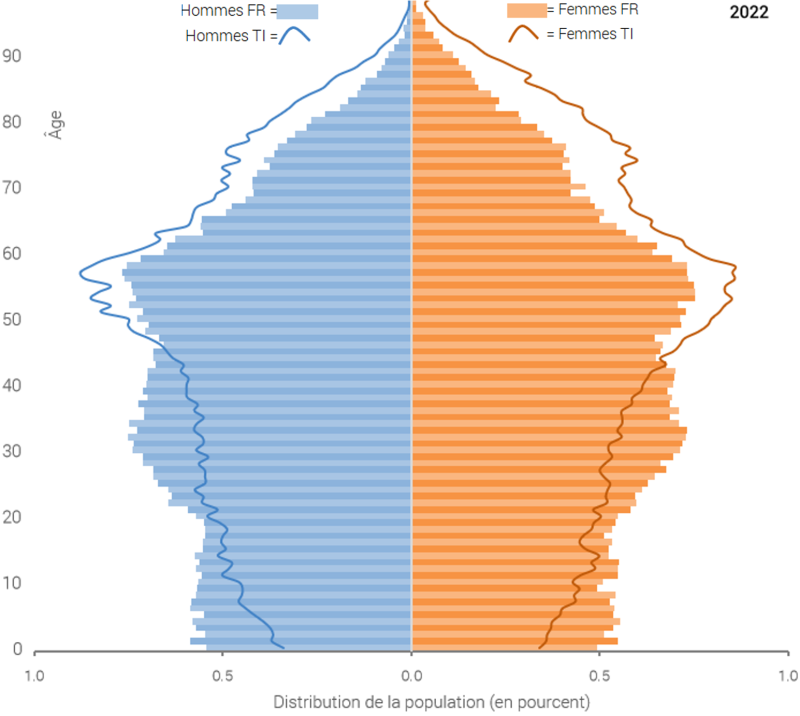
Graphique 1: Population résidante permanente des cantons de Fribourg (FR) et du Tessin (TI) au 31 décembre 2022
Source: OFS – STATPOP
Ne pas prendre en compte ces différences structurelles peut entraîner des conclusions erronées, ce qu’une standardisation permet précisément d’éviter. La standardisation est un calcul qui permet de comparer des populations présentant des différences structurelles (sur le plan régional ou temporel, p. ex.). Après la standardisation, les données ne correspondent cependant plus au nombre réel de cas ou au taux réel, ce qui doit être pris en compte lors de l’interprétation des résultats.
Pour 2022 par exemple, une standardisation entraîne pour le canton du Tessin une baisse du taux de mortalité, qui passe de 991 à 762 décès pour 100 000 habitants. Pour le canton de Fribourg, cette même standardisation provoque une hausse de ce taux de 739 à 909 décès pour 100 000 habitants. Sa population étant plus âgée, le canton du Tessin présente un taux brut (ou non standardisé) plus élevé que celui de Fribourg. Dès lors qu’on applique la même structure démographique pour les deux populations (dans notre cas la population européenne standard de 2010), la mortalité est plus faible au Tessin que dans le canton de Fribourg.
Selon quelle méthode l’Obsan standardise-t-il les indicateurs?
On recourt ici à la méthode directe. Cela signifie que l’on pondère les taux spécifiques (par âge et par sexe) par la structure d’une population standard théorique. Il devient alors possible de comparer sur une même base les résultats de différentes populations. Toutefois, conséquence quelque peu malheureuse de cette standardisation, l’accès simple et intuitif aux chiffres effectifs devient caduc.
Formule du calcul du taux standardisé selon l’âge et le sexe:
R : Taux standardisés selon l'âge et le sexe
Nij : nombre de personnes du groupe d’âge i et de sexe j dans la population standard
rij : taux brut spécifique à l’âge i et au sexe j dans la population étudiée
La population standard se réfère ici à la population standard européenne de 2010 (Eurostat, 2013).
L’intervalle de confiance, également présenté, est une mesure indiquant la précision de l’estimation. Il définit les limites dans lesquelles la valeur réelle se situe avec une probabilité de 95%. Pour les indicateurs de l’enquête suisse sur la santé (ESS), l’estimation des intervalles de confiance se base sur une linéarisation de la série de Taylor (Woodruff, 1971). Pour les autres, on se base sur une approximation de la variance des taux par la loi Gamma (Tiwari et al., 2006).
Où trouver les taux bruts et standardisés?
L’Obsan publie majoritairement des indicateurs standardisés. Cependant, il se peut qu’ils ne le soient pas, par exemple en raison d’un échantillon trop petit, de données incomplètes selon l’âge et le sexe, ou simplement parce que la standardisation n’est pas pertinente dans tous les cas.
Pour les indicateurs de l’ESS, les taux bruts (non-standardisés) sont présentés par défaut. Pour obtenir les taux standardisés selon l’âge et le sexe, il faut déplacer le curseur au-dessus du graphique. Si le curseur n’apparaît pas sur la page de l’indicateur, seuls les taux standardisés ou non standardisés sont présentés dans les graphiques. Lorsqu’un indicateur a été standardisé, les données brutes sont systématiquement disponibles dans les tableaux de données. Il suffit de cliquer sur le bouton correspondant.
Références
- Eurostat (2013). Revision of the European Standard Population — Report of Eurostat’s task force. Luxembourg: Publications Office of the European Union: Rapport (en anglais).
- Tiwari, R.C., Clegg, L.X., & Zou, Z. (2006). Efficient interval estimation for age-adjusted cancer rates. Statistical methods in medical research, 15(6), 547-569: Publication (en anglais).
- Woodruff, R.S. (1971). A Simple Method for Approximating the Variance of a Complicated Estimate. Journal of the American Statistical Association, 66:411–414: Publication (en anglais).