Standardisierung – Erklärung und Berechnung

Wie oft kommt eine bestimmte Krankheit vor? Wie hoch ist die Hospitalisierungsrate? Was sind die Kosten für das Gesundheitssystem? Viele Zahlen im Bereich der Gesundheit und des Gesundheitswesens sind nur dann aussagekräftig, wenn man die Grösse der Bevölkerung kennt, auf die sie sich beziehen. Daher werden Anteile in % oder Raten berechnet, die die Zahlen pro 1000 oder 100 000 Einwohnerinnen und Einwohner (rohe Raten) darstellen. 

Häufig interessieren Fragen nach Unterschieden zwischen Regionen oder Bevölkerungsgruppen oder nach der zeitlichen Entwicklung der Raten. Um den Effekt von unterschiedlichen Bevölkerungszusammensetzungen bei Vergleichen zu korrigieren, müssen die strukturellen Merkmale der Bevölkerung berücksichtigt werden. Im Vordergrund stehen dabei Alter und Geschlecht. So ist beispielsweise zu erwarten, dass bei einer sehr alten Bevölkerung bestimmte Krankheiten öfter vorkommen und die Hospitalisierungsrate sowie die Kosten des Gesundheitssystems höher sind als bei einer jüngeren Bevölkerung. Oder man sieht bei Frauen im gebärfähigen Alter deutlich mehr Krankenhausaufenthalte als bei gleichaltrigen Männern. 

Grosse Unterschiede in den demografischen Merkmalen einer Bevölkerung sieht man vor allem im globalen Kontext. Doch auch zwischen den Schweizer Kantonen gibt es Unterschiede. So war die Bevölkerung 2022 im Kanton Tessin mit 24% 65-Jährigen und älteren Personen zum Beispiel deutlich älter als diejenige im Kanton Freiburg (17% 65+-Jährige, vgl. Grafik 1). Eine Bevölkerung einer bestimmten Region kann sich zudem auch über die Zeit strukturell verändern. 

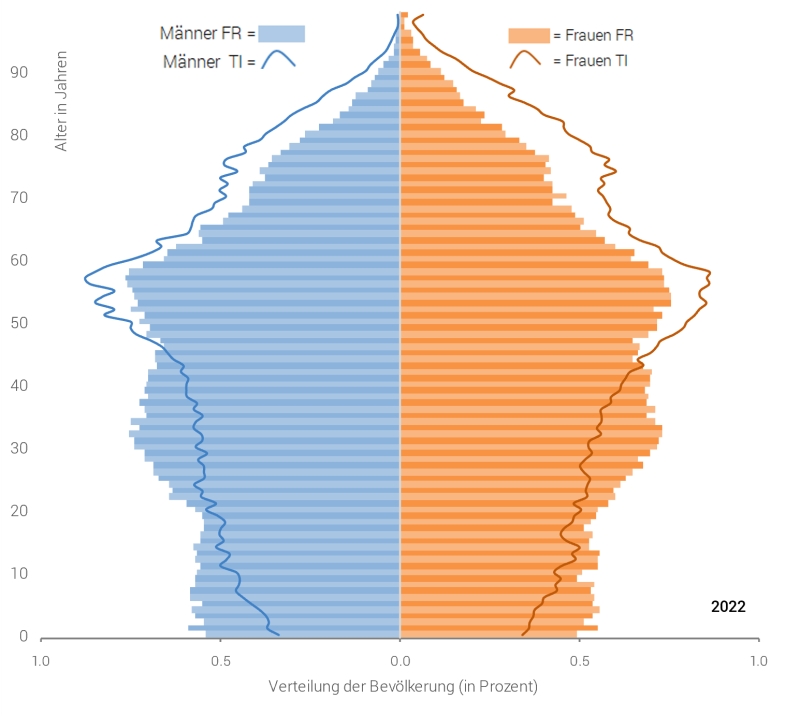
Grafik 1: Ständige Wohnbevölkerung der Kantone Freiburg (FR) und Tessin (TI) am 31.12.2022. 
Quelle: BFS – STATPOP

Werden strukturelle Unterschiede nicht berücksichtigt, kann dies zu verzerrten Schlussfolgerungen führen, was durch eine Standardisierung vermieden werden kann. Die Standardisierung ist eine Berechnung, die Vergleiche strukturell unterschiedlicher Bevölkerungen (z.B. örtlich oder zeitlich) ermöglicht. Die umgerechneten Daten entsprechen jedoch nicht mehr der tatsächlichen Anzahl Fälle oder Rate, was bei der Interpretation der Resultate berücksichtigt werden muss.

Mit einer Standardisierung vermindert sich beispielsweise die Mortalitätsrate des Kantons Tessin im Jahr 2022 von 991 auf 762 Todesfälle pro 100 000 Einwohnerinnen und Einwohner. Im Kanton Freiburg führt die Standardisierung zu einer Erhöhung der Rate von 739 auf 909 Todesfälle pro 100 000 Personen der Bevölkerung. Die höhere rohe (nicht-standardisierte) Rate im Tessin erklärt sich durch die ältere Bevölkerung verglichen mit Freiburg. Wenn beiden Bevölkerungsgruppen dieselbe demografische Struktur zugrunde gelegt wird (hier die europäische Standardbevölkerung 2010), zeigt sich im Vergleich eine geringere Mortalität im Kanton Tessin. 

Die Standardisierung wird nach der direkten Methode vorgenommen. Dies bedeutet, dass gruppenspezifische Raten nach Alter und Geschlecht berechnet und gewichtet werden, so dass sie der Bevölkerungsstruktur einer theoretischen Standardbevölkerung entsprechen. Die Resultate sind somit zwischen verschiedenen Bevölkerungsgruppen vergleichbar. Mit der Standardisierung geht jedoch der einfache, intuitive Zugriff auf die effektiven Zahlen verloren. 

Formel für die Berechnung der alters- und geschlechtsstandardisierten Raten (R):

R : Alters- und geschlechtsstandardisierte Rate
N_ij : Zahl der Personen in der Altersgruppe i und Geschlecht j in der Standardbevölkerung
r_ij : Alters- und geschlechtsspezifische rohe Rate der untersuchten Bevölkerung
Als Standardbevölkerung wird die europäische Standardpopulation 2010 (Eurostat, 2013) verwendet.

Das Vertrauensintervall, das ebenfalls gezeigt wird, ist ein Mass für die Präzision der Schätzung. Es definiert die Grenzen, innerhalb derer der wahre Wert mit einer Wahrscheinlichkeit von 95% zu finden ist. Bei den Indikatoren der Schweizerischen Gesundheitsbefragung (SGB) basiert die Schätzung der Konfidenzintervalle auf einer Linearisierung der Taylor-Reihe (Woodruff, 1971). Bei den anderen Indikatoren basiert sie auf einer Gamma-Approximation der Varianz der Rate (Tiwari et al., 2006). 

Ein bedeutender Teil der Indikatoren, die vom Obsan veröffentlicht werden, sind standardisiert. Einige werden jedoch nicht standardisiert, z.B. aufgrund einer zu kleinen Stichprobe, unvollständiger Daten nach Alter und Geschlecht oder weil eine Standardisierung nicht in allen Fällen sinnvoll ist.

Bei den Indikatoren der SGB werden standardmässig die rohen (nicht-standardisierten) Raten gezeigt. Die nach Alter und Geschlecht standardisierten Raten erscheinen durch das Verschieben des Schalters über der Grafik. Bei den Indikatoren, die über keinen entsprechenden Schalter verfügen, werden nur die standardisierten oder rohen Raten gezeigt. Bei den standardisierten Indikatoren sind die rohen Raten jedoch stets in den Datentabellen zu finden, die mit einem Klick auf den entsprechenden Button geöffnet werden können.

• Eurostat (2013). Revision of the European Standard Population – Report of Eurostat’s task force. Luxembourg: Publications Office of the European Union: Bericht (englisch). 
• Tiwari, R.C., Clegg, L.X., & Zou, Z. (2006). Efficient interval estimation for age-adjusted cancer rates. Statistical methods in medical research, 15(6), 547-569: Publikation (englisch). 
• Woodruff, R.S. (1971). A Simple Method for Approximating the Variance of a Complicated Estimate. Journal of the American Statistical Association, 66:411–414: Publikation (englisch).